广东专升本复习资料数学2--多元函数微分学知识点睛2
2、中间变量是多元函数的情形
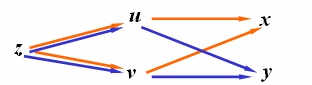
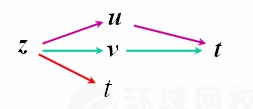
链式法则如图示:
解:
考点四:隐函数的导数和偏导数
解此题在第二章第六节采用两边求导的方法做过,这里我们直接用公式求之.
考点五:二阶偏导数(就是一阶偏导数再求偏导数)
考点六、二元函数的极值
1、二元函数的无约束极值
第一步解方程组
fx(x,y)=0,fy(x,y)=0,
求得一切实数解,即可得一切驻点.
第二步对于每一个驻点(x0,y0),求出二阶偏导数的值
第三步定出AC-B2的符号,按定理2的结论判定f(x0,y0)是否是极值、是极大值还是极小值.
2、条件极值拉格朗日乘数法
要找函数z=f(x,y)在条件j(x,y)=0下的可能极值点,可以先构成辅助函数
F(x, y)=f(x, y)+lj(x, y) ,
其中l为某一常数。然后解方程组:
由这方程组解出x,y及l,则其中(x,y)就是所要求的可能的极值点。
典型例题求表面积为a2而体积为最大的长方体的体积.
解设长方体的三棱的长为x,y,z,则问题就是在条件
2(xy+yz+xz)=a2
下求函数V=xyz的最大值.
构成辅助函数
F(x,y,z)=xyz+l(2xy+2yz+2xz-a2),
解方程组
这是唯一可能的极值点.因为由问题本身可知最大值一定存在,
本文标签:广东省成考网高等数学二广东专升本复习资料数学2--多元函数微分学知识点睛2
转载请注明:文章转载自(http://www.gdcrgkw.cn)
⊙小编提示:添加【广东省成考网】招生老师微信,即可了解2024年广东成人高考政策资讯、成人高考报名流程、准考证打印方法、成绩查询时间以及领取历年真题资料、个人专属备考方案等相关信息!

(添加“广东省成考网”招生老师微信,在线咨询报名报考等相关问题)
《广东省成考网》免责声明:
1、由于各方面情况的调整与变化,本网提供的考试信息仅供参考,考试信息以省考试院及院校官方发布的信息为准。
2、本网信息来源为其他媒体的稿件转载,免费转载出于非商业性学习目的,版权归原作者所有,如有内容与版权问题等请与本站联系。联系邮箱:812379481@qq.com。







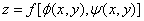
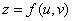
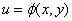
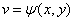
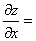
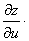
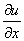
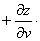
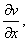
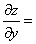
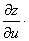
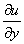
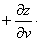
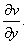
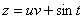
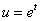
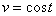
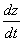
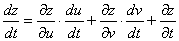
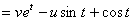
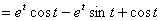
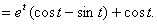
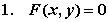
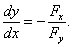
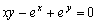
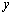
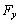
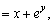
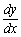
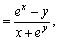
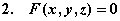
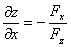
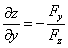
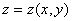
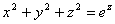
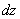
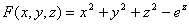
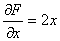
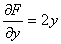
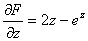
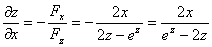
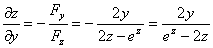
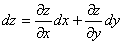
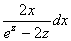
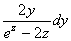
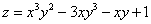
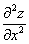
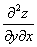
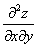
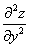
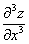
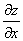
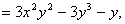
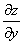
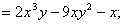
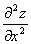
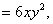
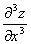
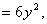
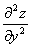
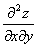
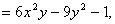
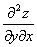
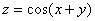
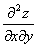
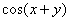
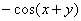
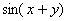
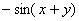
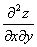
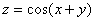
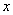
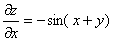
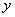
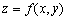
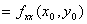
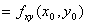
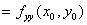
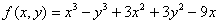
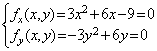
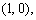
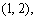
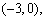
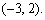
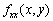
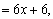
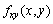
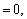
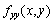
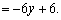
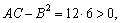
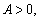
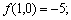
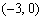
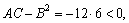
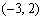
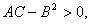
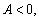
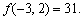
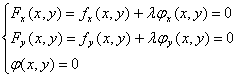
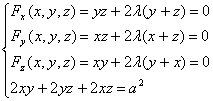
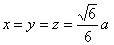
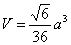








 ×
×