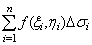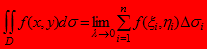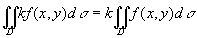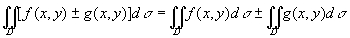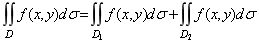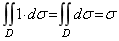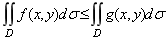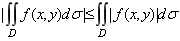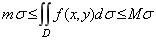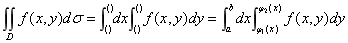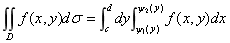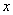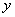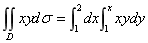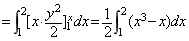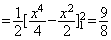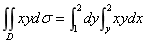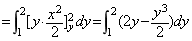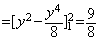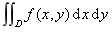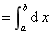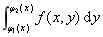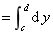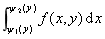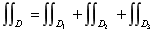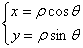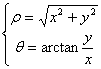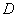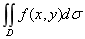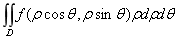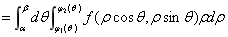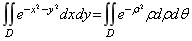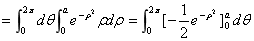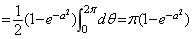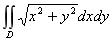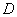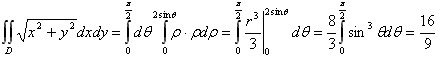广东考试复习资料数学2--多元函数积分学

多元函数积分学

知识结构：

必备基础知识

★ 二重积分的定义 

设f(x, y)是有界闭区域D上的有界函数。将闭区域D任意分成n个小闭区域：Ds ₁, Ds ₂, × × × , Ds _n ，其中Ds _i表示第i个小区域, 也表示它的面积. 在每个Ds _i上任取一点(x _i, h_i), 作和：

.   

如果当各小闭区域的直径中的最大值l趋于零时, 这和的极限总存在, 则称此极限为函数f(x, y)在闭区域D上的二重积分, 记作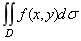, 即

.

f(x, y)被积函数, f(x, y)ds被积表达式, ds面积元素, x, y积分变量, D积分区域, 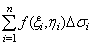积分和. 

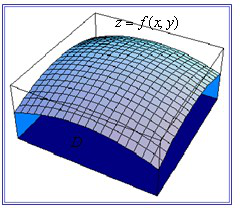
★ 二重积分的几何意义

如果f(x, y)³0, 被积函数f(x, y)可解释为曲顶柱体的在点(x, y)处的竖坐标, 所以二重积分的几何意义就是柱体的体积. 如果f(x, y)是负的, 柱体就在xOy 面的下方, 二重积分的绝对值仍等于柱体的体积, 但二重积分的值是负的.

★ 二重积分的性质（二重积分与定积分有类似的性质）

性质1 被积函数的常数因子可以提到二重积分号的外面，即

（k为常数）。

性质2 函数的和（或差）的二重积分等于各个函数的二重积分的和（或差）。

。

性质3 如果闭区域D被有限条曲线分为有限个部分闭区域，则在D上的二重积分等于在各部分闭区域上的二重积分的和。例如D分为两个闭区域D₁与 D₂，则

。

此性质表示二重积分对于积分区域具有可加性。

性质4 如果在D上，f（x，y）= 1，s 为D的面积，则

。

此性质的几何意义很明显，因为高为1的平顶柱体的体积在数值上就等于柱体的底面积。

性质5：如果在D上, f (x, y)£g(x, y), 则有不等式：

特殊地，

性质6设M、m分别是f(x, y)在闭区域D上的最大值和最小值, s为D的面积, 则有：        

.

上述不等式是对二重积分估值的不等式。

性质7（二重积分的中值定理）设函数f(x, y)在闭区域D上连续, s 为D的面积, 则在D上至少存在一点(x, h)使得：.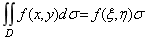 

★ 积分区域的分类

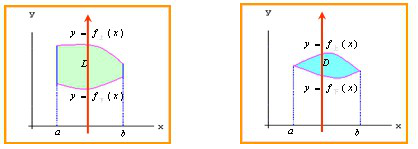
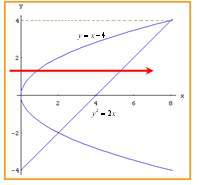
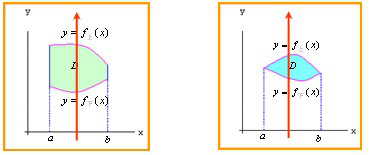
（1）上下结构：平面图形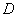由上下两条曲线y=f_上(x)与y=f_下(x)及左右两条直线x=a与x=b所围成

特点：

（1）平面图形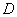上下是两条曲线y=f_上(x)和y=f_下(x)，左右是两条直线x=a与x=b；

（2）作穿过平面图形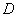且平行于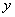轴的有向直线，进入区域交的是y=f_下(x)，出来区域交的是y=f_上(x)

例：抛物线、所围成的图形

解：该平面图形为上下结构：

上面是曲线：；

下面是曲线：；

左边是直线：；

右边是直线：。

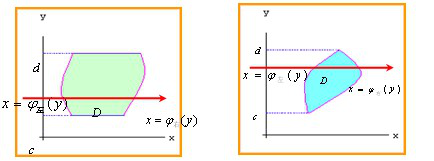
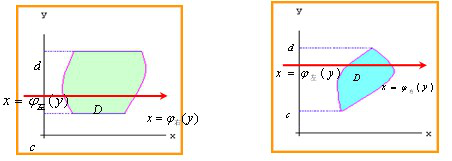
（2）左右结构：平面图形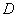由左右两条曲线x=j_左(y)与x=j_右(y)及上下两条直线y=d与y=c所围成。

特点：

（1）平面图形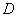左右是两条曲线x=j_左(y)和x=j_右(y)，上下是两条直线y=d与y=c；

（2）作穿过平面图形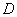且平行于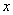轴的有向直线，进入区域交的是x=j_左(y)，出来区域交的是x=j_右(y)。

例：由曲线和直线所围成的图形

解：该平面图形为左右结构：             

左边是曲线：；

右边是曲线：；

上面是直线：；

下面是直线：。

主要考察知识点和典型例题：

二重积分是定积分的扩展，是二元函数的积分，具有和定积分相似的定义和性质。从考试的角度看，主要是考查二重积分的计算，考查方法是直接给定一个二重积分，让我们选择合适的方法进行计算。

二重积分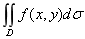的计算首先要确定坐标系，即：是在直角坐标系下还是在极坐标系下计算，两种情况往年都考过，所以都需要大家掌握。

（1）当二重积分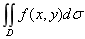的积分区域为圆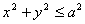面、环面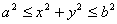、扇面等区域时，考虑用极坐标；当被积函数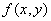含有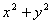、、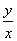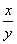也要考虑极坐标。

（2）其余情况一般考虑在直角坐标系下计算。

考点一：利用直角坐标计算二重积分（转化为二次积分）

1、上下结构区域:   D :  j₁(x)£y£j₂(x), a£x£b .

（先后）

法则：前看端点，后作平行

（2）左右结构区域:   D :  y₁(y)£ x£y₂(y), c£y£d

（先后）

法则：前看端点，后作平行

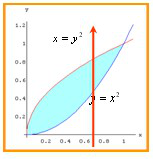
典型例题  计算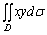, 其中D是由直线y=1、x=2及y=x所围成的闭区域. 

解: 

方法一. 可把D看成是上下结构区域: 1£x£2, 1£y£x . 于是

. 

方法二. 也可把D看成是左右结构区域: 1£y£2, y£x£2 . 于是

. 

【注】:

 (1) 若积分区域既是 上下结构区域又是左右结构区域 , 则有

为计算方便,可选择积分序, 必要时还可以交换积分序.

(2) 若积分域较复杂,可将它分成若干上下结构域或左右结构域 , 则

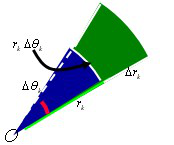
考点二： 利用极坐标计算二重积分（转化为二次积分）

若积分区域可表示为：

a£q£b, j ₁(q)£r£j ₂(q),则

＝.

典型例题：计算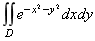, 其中D是由中心在原点、半径为a 的圆周所围成的闭区域. 

解  在极坐标系中, 闭区域D可表示为

0£r£a , 0£q £2p . 

于是  

. 

往年真题：计算，其中为与的公共部分。                  

解：在极坐标系中, 闭区域D可表示为

0£q £，0£r £ , 

于是