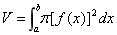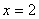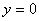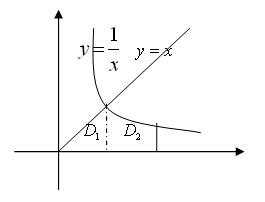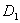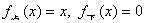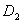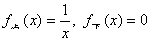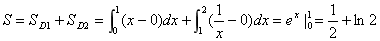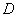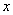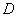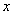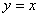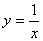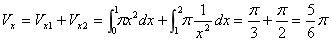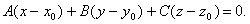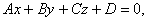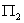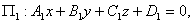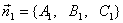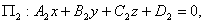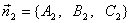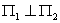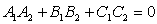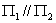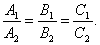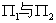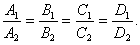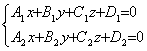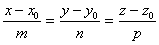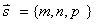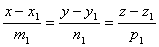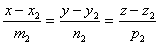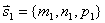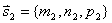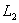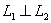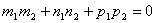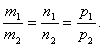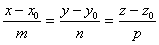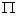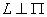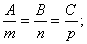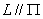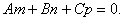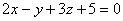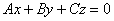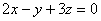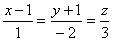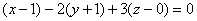广东成人高考复习资料数学2--一元函数积分学知识点睛

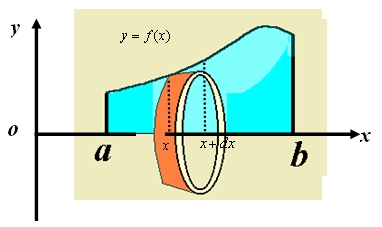
考点二：旋转体的体积

旋转体的体积为：.

注：求旋转体的体积，关键在于确定边缘曲线，其实就是与旋转轴相对的那条曲线。

典型例题（1）求曲线、、，所围成的平面图形的面积。

解(1)画图（可以看成上下结构），

把图形拆成和。

(2)确定在x轴上的投影区间:[0,1],[1,2].

(3)确定上下曲线:  

：.

：

(4)计算积分

（2）：求（1）中平面图形绕轴旋转一周所成旋转体的体积。

解：平面图形绕轴旋转，其边缘曲线由两条，分别为：与。

旋转体的体积为：。

空间解析几何

必备基础知识

★平面的点法式方程

n=(A,B,C),

★平面的一般方程

n=(A,B,C),

★特殊的平面方程（缺谁就平行于谁）

Ax+By+Cz=0：D=0,平面过原点.

By+Cz+D=0：n=(0,B,C),法线向量垂直于x轴,平面平行于x轴.

Ax+Cz+D=0：n=(A,0,C),法线向量垂直于y轴,平面平行于y轴.

Ax+By+D=0：n=(A,B,0),法线向量垂直于z轴,平面平行于z轴.

Cz+D=0：n=(0,0,C),法线向量垂直于x轴和y轴,平面平行于xOy平面.

Ax+D=0：n=(A,0,0),法线向量垂直于y轴和z轴,平面平行于yOz平面.

By+D=0：n=(0,B,0),法线向量垂直于x轴和z轴,平面平行于zOx平面.

★平面的关系

设有两平面和：

可推出：

（1）的充要条件是；

（2）的充要条件是

（3）重合的充要条件是

★空间直线的一般方程（就是两个平面方程构成的方程组）

.(1)

★空间直线的对称式方程（关键是找到一个点和一个方向向量）

.    

★直线的关系

设有两直线：

L₁:,L₂:,

其中，分别是直线，的方向向量，则：

（1）的充要条件是；

（2）的充要条件是

★直线与平面的关系

设有一条直线和一个平面，其方程分别为：

：

：

直线的方向向量s=(m,n,p),平面的法线向量为n=(A,B,C),则：

（1）的充要条件是

（2）的充要条件是

★简单的二次曲面

主要考察知识点和典型例题：

考点一：求平面的方程

典型例题求通过x轴和点(4,-3,-1)的平面的方程.

解平面通过x轴,一方面表明它的法线向量垂直于x轴, 即A=0;另一方面表明 它必通过原点,即D=0.因此可设这平面的方程为

By+Cz=0.

又因为这平面通过点(4,-3,-1),所以有

-3B-C=0,或C=-3B.

将其代入所设方程并除以B(B¹0),便得所求的平面方程为

y-3z=0.

往年真题：过原点且与平面平行的平面方程为_______。

解：由于平面通过原点，即D=0。因此可设这平面的方程为：

又因为所求平面与已知平面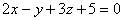平行，所以已知平面的法向量n=(2，－1，3)可以作为所求平面的法向量，即：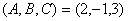

所以平面方程为：

考点二：求直线方程

典型例题求过点(1,-2,4)且与平面2x-3y+z-4=0垂直的直线方程.

解 平面的法线向量n＝(2,-3,1)可以作为所求直线的方向向量s.由此可得所求直线的方程为.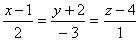

往年真题：过点（1，－1，0）与直线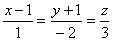垂直的平面方程为_____。

解：因为所求的平面与直线垂直，所以，直线的方向向量

s=(1，－2，3)可以看作所求平面的法向量n。

又因为所求平面过点（1，－1，0），所以由平面的点法式方程得：

。